This approximate method describes the propagation of light through rectangular dielectric waveguides. Marcatili's original approach is valid for low-index-contrast waveguides, and we extended the method to the regime of high-index-contrast waveguides by adjusting the amplitudes of the components of the electromagnetic fields [1,2]. In this article, we consider typical waveguides in silicon-on-insulator (SOI) technology which are 220 nm high. Silicon photonic integrated circuits with 220 nm high rectangular waveguides have gained large interest. Several microelectronic research institutes have tailored CMOS processes and now offer wafer-scale fabrication [3].

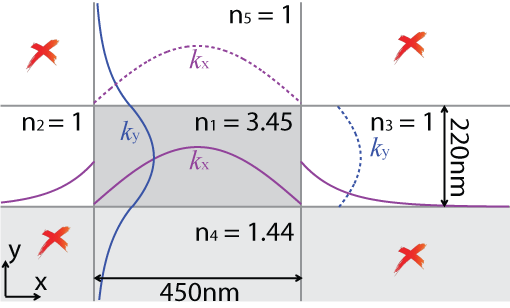
Fig 1. Definition of the SOI waveguide (grayscale) and sketch of modal field.

Figure 1 shows a cross-section of the waveguide. We consider a propagating wave with the electric field in the form E(x,y) = exp[i(ωt - βz)]. It is assumed that most of its energy is in the center of the guide, and that the mode is “TE-like” with the majority of the energy in E_x and H_y. From this we make the Ansatz that E_x(x,y), and H_y(x,y), are proportional to cos[k_x(x + ξ)] cos[k_y(y + η)], with maximum field in the center. Outside the core, the fields decay exponentially, while the transversal profile of the field is identical to that in the core (Fig. 1). The outer quadrants are neglected because the fields are small in those regions. We choose to obey Maxwell's equations in all regions 1-5 (Fig 1), so that all errors of the approximation manifest themselves at the interfaces.

At the interfaces of the core of the waveguide, continuity of the tangential electromagnetic field components is required, adding up to 4 × 4 = 16 conditions. The Ansatz has 13 free parameters, and no solution that exactly obeys all conditions. Thus approximations are necessary.

It is argued that the dominant boundary conditions for determining k_y are at the horizontal interfaces, while the vertical interfaces dominate k_x. This gives the propagation constant β² = k₀²n₁² - k_x² - k_y². This approximation is accurate within 1% (Fig 2a).

For low-index-contrast waveguides k₀n_j ≈ β because modes are not guided otherwise, so k_x ≈ k_y << 1. Marcatili's method neglects these terms in the second order, while these terms can be larger than unity for SOI guides.

We proposed the Extended E_y ≈ 0 method [2] in which the fields are continuous at the horizontal interfaces. At the vertical interfaces, E_x and H_z are matched, while E_z and H_x are not. E_xis a dominant component, H_z is chosen over E_z because an infinitely wide (slab) waveguide has E_z = 0, and H_x is a weak field component with high intensity at the corners of the guide.

We also proposed the amplitude optimization method [2] in which the energy density associated with the discontinuity of the tangential field across the interfaces is minimized.

For 400 nm × 220 nm SOI waveguides, the error in effective index is below 1%. The modal fields from Marcatili E_y = 0, the Extended E_y ≈ 0 and the amplitude optimization methods show a difference with rigorous calculations of 4.4%, 2.2%, and 1.8% (in energy), respectively. Marcatili's method is widely used. And with our work, the development of intuitive analytical methods now follows the technological developments.

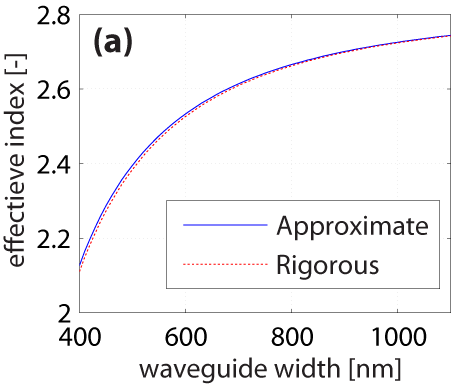
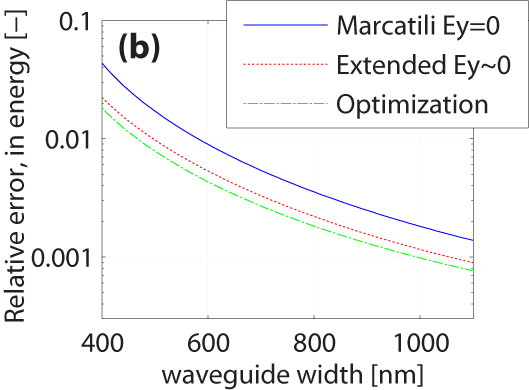
Fig 2. Results compared with rigorous mode solver (film mode matching method in FimmWave, Photon Design, Oxford UK) [4]. (a) Effective index. (b) Energy in the difference field between the approximate methods and the rigorously computed field, normalized.